Trigonometri nedir , matematiğin bir dalıdır ve üçgenlerin özelliklerini inceleyen bir bilim dalıdır. Kelime kökeni “üçgen ölçümü” anlamına gelen Yunanca “trigonon” ve “metron” kelimelerinden gelir.
Trigonometri, özellikle geometri, fizik, mühendislik ve astronomi gibi diğer bilim dallarında çok önemli bir rol oynar. Üçgenlerin açıları ve kenar uzunlukları arasındaki ilişkileri inceler. Trigonometri, trigonometrik fonksiyonlar olarak adlandırılan matematiksel fonksiyonlarla ilgilidir.
Üçgenlerin iç açıları toplamı 180 derecedir. Trigonometri, üçgenlerin açılarını veya kenar uzunluklarını verildiğinde, diğer açıları veya kenar uzunluklarını hesaplamak için kullanılır. Trigonometrik fonksiyonlar, sinüs, kosinüs ve tanjant gibi, açıların ve kenar uzunluklarının birbirleriyle olan ilişkilerini ifade eder.
Sinüs, bir üçgenin bir açısının karşısındaki kenarın üçgenin hipotenüsüne oranıdır. Kosinüs, bir üçgenin bir açısının bitişik kenarının hipotenüse oranıdır. Tanjant ise, bir üçgenin bir açısının karşısındaki kenarının bitişik kenara oranıdır.
Trigonometri, dairesel fonksiyonlar olarak da ifade edilebilir. Dairesel fonksiyonlar, birim çember üzerinde bir noktanın x ve y koordinatlarını ifade eder. Bu, trigonometrik fonksiyonlarla ilişkili bir açıya karşılık gelir. Trigonometrik fonksiyonlar, dairesel fonksiyonlarla birbirlerine dönüştürülebilir.
Trigonometri, matematiksel bir konu olduğu kadar, pratik uygulamalar için de önemlidir. Mühendislik, inşaat, fizik ve diğer bilim dallarında trigonometri, problemleri çözmek için kullanılan temel bir araçtır. Örneğin, bir mühendis bir binanın yüksekliğini hesaplamak için trigonometri kullanabilir.
Trigonometri Temel Formüller
Trigonometri, matematiğin önemli bir dalıdır ve açılar, üçgenler ve daireler gibi geometrik şekillerle ilgilidir.
Sinüs Formülü
Sinüs formülü, bir üçgenin açılarını ve kenar uzunluklarını ilişkilendirir. Formül şöyle ifade edilir:
sin A / a = sin B / b = sin C / c
Burada, A, B ve C, üçgenin iç açılarıdır, a, b ve c ise üçgenin karşıt kenarlarının uzunluklarıdır. Formül, herhangi bir açının sinüsünün, o açıya karşı gelen kenarın uzunluğu ile diğer iki açının sinüslerinin çarpımının oranına eşit olduğunu ifade eder.
Kosinüs Formülü
Kosinüs formülü, bir üçgenin açıları ve kenar uzunlukları arasındaki ilişkiyi ifade eder. Formül şöyle ifade edilir:
c² = a² + b² – 2ab cos C
Burada, a, b ve c, üçgenin kenar uzunluklarıdır ve C, üçgenin karşıt açısıdır. Formül, bir üçgenin bir kenarının uzunluğunu ve iki diğer kenarın uzunluklarını bilerek, açının kosinüsünü hesaplamak için kullanılır.
Tanjant Formülü
Tanjant formülü, bir açının tanjantını, o açıya karşı gelen kenarların oranı olarak ifade eder. Formül şöyle ifade edilir:
tan A = a / b
Burada, A, üçgenin bir açısıdır, a, A açısına karşı gelen kenarın uzunluğudur ve b, A açısı ile diğer açıların arasında kalan kenarın uzunluğudur.
Kotanjant Formülü
Kotanjant formülü, bir açının kotanjantını, o açıya karşı gelen kenarların ters oranı olarak ifade eder. Formül şöyle ifade edilir:
cot A = b / a
Burada, A, üçgenin bir açısıdır, b, A açısına karşı gelen kenarın uzunluğudur ve a, A açısı ile diğer açıların arasında kalan kenarın uzunluğudur.
Dairesel Trigonometri Formülleri
Dairesel trigonometri, birim çember üzerindeki bir noktanın koordinatlarını ve açılarını inceler. Bu alanın temel formülleri şunlardır:
sin θ = y / r cos θ = x / r tan θ = y / x cot θ = x / y
Burada, θ, açının ölçüsüdür, r, birim çemberin yarıçapıdır, x ve y, noktanın koordinatlarıdır. Sinüs, kosinüs, tanjant ve cotanjant, dairesel trigonometri formülleri olarak ifade edilir.
Ters Trigonometri Formülleri
Ters trigonometri formülleri, bir açının sinüsü, kosinüsü veya tanjantı verildiğinde, o açının ölçüsünü hesaplamak için kullanılır. Bu formüller şunlardır:
sin⁻¹ (x) = θ cos⁻¹ (x) = θ tan⁻¹ (x) = θ
Burada, x, sinüs, kosinüs veya tanjantın değeridir, θ ise açının ölçüsüdür.
Hipotenüs Formülü
Hipotenüs formülü, bir dik üçgenin hipotenüsünü hesaplamak için kullanılır. Formül şöyle ifade edilir:
c = √(a² + b²)
Burada, a ve b, dik üçgenin diğer iki kenarıdır ve c, hipotenüsün uzunluğudur.
İkizkenar Üçgen Formülü
İkizkenar üçgen formülü, bir ikizkenar üçgenin alanını hesaplamak için kullanılır. Formül şöyle ifade edilir:
A = (1/2) b h
Burada, A, üçgenin alanıdır, b, üçgenin taban uzunluğudur ve h, üçgenin yüksekliğidir.
Trigonometri Tablosu
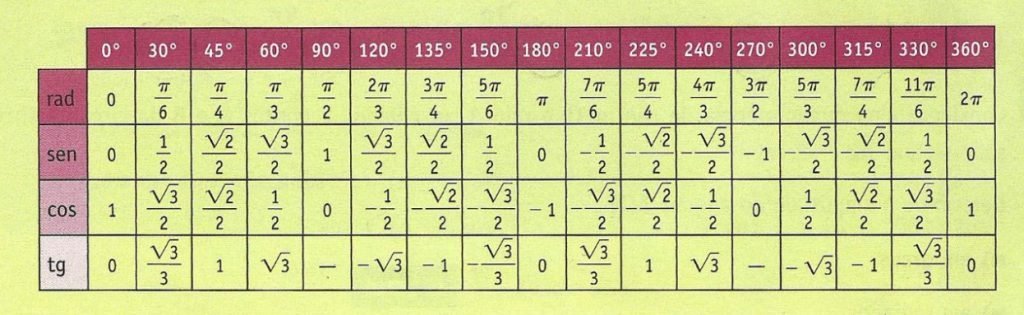
Trigonometrik fonksiyonların değerlerinin bir listesidir ve matematiksel hesaplama ve problemleri çözmek için kullanılır.
Trigonometrik fonksiyonlar, sinüs, kosinüs, tanjant, cotanjant, sekant ve kosekant gibi matematiksel fonksiyonlardır. Bu fonksiyonlar, bir açının ölçüsüne göre, o açının karşısındaki veya bitişik kenarın uzunluğunun diğer kenarın uzunluğuna bölünmesiyle hesaplanır. Trigonometrik fonksiyonların değerleri, birim çember üzerinde bir noktanın x ve y koordinatlarını ifade eder.
Trigonometri tablosu, trigonometrik fonksiyonların değerlerinin bir listesini içerir. Bu tablo, trigonometrik fonksiyonların önceden hesaplanmış değerlerini sağlar, böylece matematiksel hesaplamaları hızlandırır ve kolaylaştırır. Trigonometri tablosu, her açı için sinüs, kosinüs, tanjant, cotanjant, sekant ve kosekant fonksiyonlarının değerlerini içerir.
Trigonometri tablosunun kullanımı oldukça kolaydır. Öncelikle, hesaplanması gereken açının ölçüsü belirlenir. Daha sonra, tablodan ilgili açıya karşılık gelen sinüs, kosinüs, tanjant, cotanjant, sekant veya kosekant fonksiyonunun değeri bulunur. Bu değer, matematiksel hesaplamalarda kullanılır veya problemin çözümüne yardımcı olur.
Trigonometrik Fonksiyonlar
Sinüs Fonksiyonu
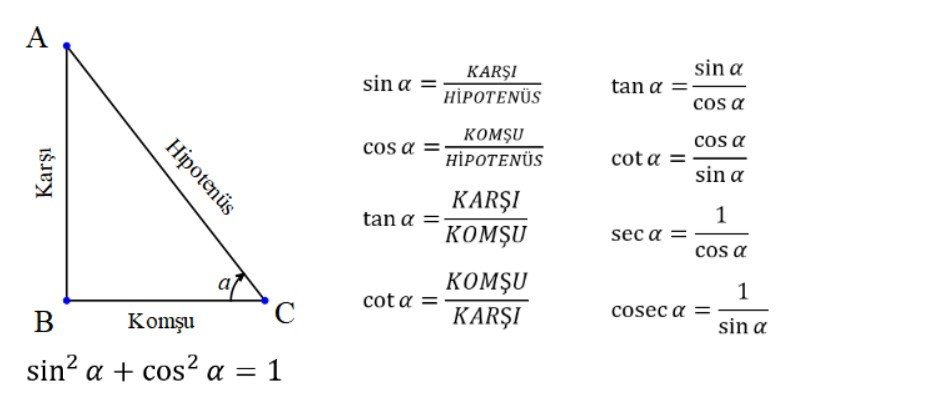

Sinüs fonksiyonu, trigonometrik fonksiyonlar arasında en temel olanıdır. Bu fonksiyon, açının ölçüsüne göre, o açının karşısındaki kenarın hipotenüse olan oranını ifade eder. Sinüs fonksiyonu, matematik, fizik, mühendislik ve diğer bilim dallarında sıklıkla kullanılır.
Sinüs fonksiyonu, matematiksel olarak şu şekilde ifade edilir:
sin(x) = opposite / hypotenuse
Burada, x açının ölçüsüdür, opposite ise x açısına karşı gelen kenarın uzunluğudur ve hypotenuse ise üçgenin hipotenüsünün uzunluğudur. Sinüs fonksiyonunun değeri, x açısının ölçüsüne bağlıdır. Örneğin, sin(30°) = 0.5, sin(60°) = √3/2 ve sin(90°) = 1 olarak hesaplanır.
Sinüs fonksiyonu, birçok trigonometrik ilişkiyi ifade etmek için kullanılır. Örneğin, sinüs fonksiyonu, bir üçgenin iç açıları ve kenar uzunlukları arasındaki ilişkiyi ifade eden sinüs formülü ile ilişkilidir. Ayrıca, dairesel trigonometri için de önemlidir, çünkü sinüs fonksiyonu, birim çember üzerindeki bir noktanın y koordinatını ifade eder.
Sinüs fonksiyonu, ayrıca dalga hareketlerinin matematiksel modellerinde de kullanılır. Örneğin, bir ses dalgasının matematiksel modelinde, sinüs fonksiyonu ses dalgalanmalarını ifade etmek için kullanılır.
Sinüs fonksiyonunun grafiği, bir dalga formu olarak görülebilir. Grafik, x ekseninde açının ölçüsünü ve y ekseninde sinüs fonksiyonunun değerini gösterir. Sinüs fonksiyonunun grafiği, periyodik bir şekilde tekrarlanan dalga formuna sahiptir ve dalga boyu, tepe noktası ve dip noktası gibi özelliklere sahiptir.
Kosinüs Fonksiyonu

Kosinüs fonksiyonu, trigonometrik fonksiyonlar arasında en temel olanlarından biridir. Bu fonksiyon, açının ölçüsüne göre, o açının bitişik kenarının hipotenüse olan oranını ifade eder. Kosinüs fonksiyonu, matematik, fizik, mühendislik ve diğer bilim dallarında sıklıkla kullanılır.
Kosinüs fonksiyonu, matematiksel olarak şu şekilde ifade edilir:
cos(x) = adjacent / hypotenuse
Burada, x açının ölçüsüdür, adjacent ise x açısına bitişik olan kenarın uzunluğudur ve hypotenuse ise üçgenin hipotenüsünün uzunluğudur. Kosinüs fonksiyonunun değeri, x açısının ölçüsüne bağlıdır. Örneğin, cos(30°) = √3/2, cos(60°) = 0.5 ve cos(90°) = 0 olarak hesaplanır.
Kosinüs fonksiyonu, birçok trigonometrik ilişkiyi ifade etmek için kullanılır. Örneğin, kosinüs fonksiyonu, bir üçgenin iç açıları ve kenar uzunlukları arasındaki ilişkiyi ifade eden kosinüs formülü ile ilişkilidir. Ayrıca, dairesel trigonometri için de önemlidir, çünkü kosinüs fonksiyonu, birim çember üzerindeki bir noktanın x koordinatını ifade eder.
Kosinüs fonksiyonu, ayrıca doğrusal hareket problemlerinde ve vektör hesaplamalarında da kullanılır. Örneğin, bir nesnenin hızını veya yönünü hesaplamak için kosinüs fonksiyonu kullanılabilir.
Kosinüs fonksiyonunun grafiği, cos(x) = y şeklinde ifade edilir ve x ekseninde açının ölçüsünü, y ekseninde ise kosinüs fonksiyonunun değerini gösterir. Kosinüs fonksiyonunun grafiği, sinüs fonksiyonunun grafiğine benzer şekilde periyodik bir dalga formuna sahiptir ve dalga boyu, tepe noktası ve dip noktası gibi özelliklere sahiptir.
Tanjant Fonksiyonu
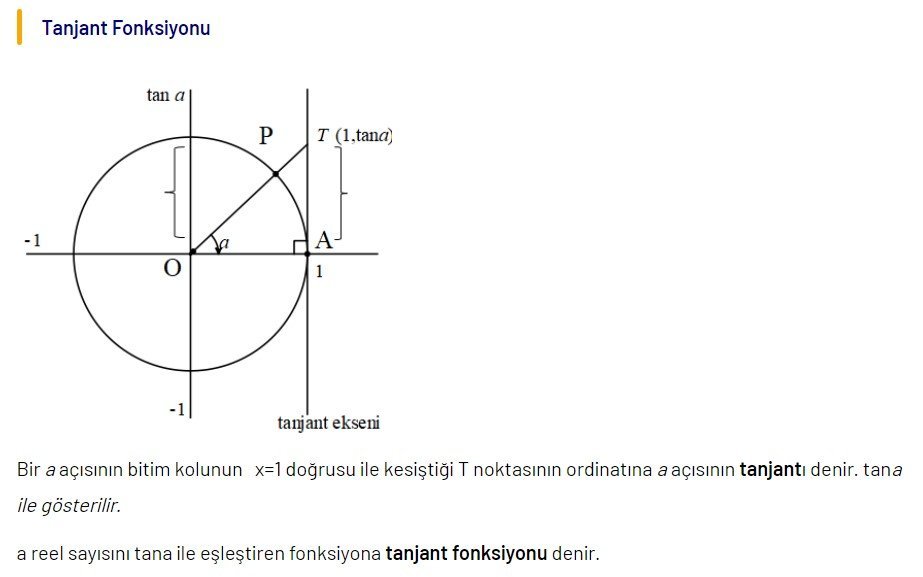

Tanjant fonksiyonu, trigonometrik fonksiyonlar arasında önemli olan biridir. Bu fonksiyon, açının ölçüsüne göre, o açının karşısındaki kenarın bitişik kenara olan oranını ifade eder. Tanjant fonksiyonu, matematik, fizik, mühendislik ve diğer bilim dallarında sıklıkla kullanılır.
Tanjant fonksiyonu, matematiksel olarak şu şekilde ifade edilir:
tan(x) = opposite / adjacent
Burada, x açının ölçüsüdür, opposite ise x açısına karşı gelen kenarın uzunluğudur ve adjacent ise x açısına bitişik olan kenarın uzunluğudur. Tanjant fonksiyonunun değeri, x açısının ölçüsüne bağlıdır. Örneğin, tan(30°) = 1/√3, tan(60°) = √3 ve tan(45°) = 1 olarak hesaplanır.
Tanjant fonksiyonu, birçok trigonometrik ilişkiyi ifade etmek için kullanılır. Örneğin, tanjant fonksiyonu, bir üçgenin iç açıları ve kenar uzunlukları arasındaki ilişkiyi ifade eden tanjant formülü ile ilişkilidir. Ayrıca, dairesel trigonometri için de önemlidir, çünkü tanjant fonksiyonu, birim çember üzerindeki bir noktanın y koordinatının x koordinatına olan oranını ifade eder.
Tanjant fonksiyonu, ayrıca açısal hız ve açısal ivme gibi kavramların hesaplamalarında kullanılır. Örneğin, bir nesnenin açısal hızını hesaplamak için tanjant fonksiyonu kullanılabilir.
Tanjant fonksiyonunun grafiği, tan(x) = y şeklinde ifade edilir ve x ekseninde açının ölçüsünü, y ekseninde ise tanjant fonksiyonunun değerini gösterir. Tanjant fonksiyonunun grafiği, sınır noktalarında sonsuzluğa yaklaşır ve dalgalı bir yapıya sahiptir.
Kotanjant Fonksiyonu

Kotanjant fonksiyonu, trigonometrik fonksiyonlar arasında önemli olan biridir. Bu fonksiyon, açının ölçüsüne göre, o açının bitişik kenarının karşısındaki kenara olan oranının tersini ifade eder. Kotanjant fonksiyonu, matematik, fizik, mühendislik ve diğer bilim dallarında sıklıkla kullanılır.
Kotanjant fonksiyonu, matematiksel olarak şu şekilde ifade edilir:
cot(x) = adjacent / opposite
Burada, x açının ölçüsüdür, adjacent ise x açısına bitişik olan kenarın uzunluğudur ve opposite ise x açısına karşı gelen kenarın uzunluğudur. Kotanjant fonksiyonunun değeri, x açısının ölçüsüne bağlıdır. Örneğin, cot(30°) = √3, cot(60°) = 1/√3 ve cot(45°) = 1 olarak hesaplanır.
Kotanjant fonksiyonu, birçok trigonometrik ilişkiyi ifade etmek için kullanılır. Örneğin, kotanjant fonksiyonu, bir üçgenin iç açıları ve kenar uzunlukları arasındaki ilişkiyi ifade eden kotanjant formülü ile ilişkilidir. Ayrıca, dairesel trigonometri için de önemlidir, çünkü kotanjant fonksiyonu, birim çember üzerindeki bir noktanın x koordinatına y koordinatının oranının tersini ifade eder.
Kotanjant fonksiyonu, ayrıca elektrik devreleri ve manyetizma gibi konularda da kullanılır. Örneğin, bir manyetik alanın yönünü hesaplamak için kotanjant fonksiyonu kullanılabilir.
Kotanjant fonksiyonunun grafiği, cot(x) = y şeklinde ifade edilir ve x ekseninde açının ölçüsünü, y ekseninde ise kotanjant fonksiyonunun değerini gösterir. Kotanjant fonksiyonunun grafiği, tanjant fonksiyonunun grafiğine benzer şekilde dalgalı bir yapıya sahiptir.
Sekant Fonksiyonu
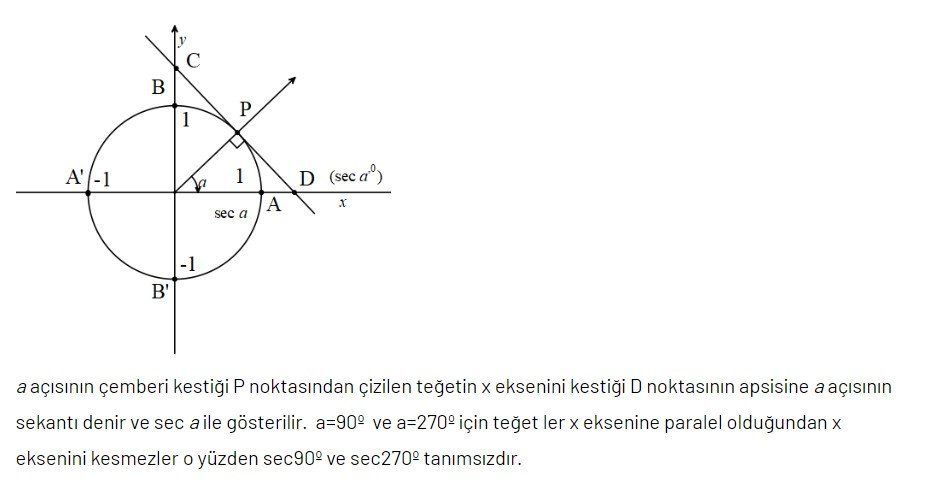
Sekant fonksiyonu, trigonometrik fonksiyonlar arasında önemli olan biridir. Bu fonksiyon, açının ölçüsüne göre, o açının hipotenüse olan oranının tersini ifade eder. Sekant fonksiyonu, matematik, fizik, mühendislik ve diğer bilim dallarında sıklıkla kullanılır.
Sekant fonksiyonu, matematiksel olarak şu şekilde ifade edilir:
sec(x) = hypotenuse / adjacent
Burada, x açının ölçüsüdür, hypotenuse ise üçgenin hipotenüsünün uzunluğudur ve adjacent ise x açısına bitişik olan kenarın uzunluğudur. Sekant fonksiyonunun değeri, x açısının ölçüsüne bağlıdır. Örneğin, sec(30°) = 2/√3, sec(60°) = 2 ve sec(45°) = √2 olarak hesaplanır.
Sekant fonksiyonu, birçok trigonometrik ilişkiyi ifade etmek için kullanılır. Örneğin, sekant fonksiyonu, bir üçgenin iç açıları ve kenar uzunlukları arasındaki ilişkiyi ifade eden sekant formülü ile ilişkilidir. Ayrıca, dairesel trigonometri için de önemlidir, çünkü sekant fonksiyonu, birim çember üzerindeki bir noktanın x koordinatının hipotenüse olan oranının tersini ifade eder.
Sekant fonksiyonu, ayrıca optik ve ışık dalga hareketleri gibi konularda da kullanılır. Örneğin, bir ışık dalga hareketinin matematiksel modelinde, sekant fonksiyonu ışık dalgasının şiddetini ifade etmek için kullanılır.
Sekant fonksiyonunun grafiği, sec(x) = y şeklinde ifade edilir ve x ekseninde açının ölçüsünü, y ekseninde ise sekant fonksiyonunun değerini gösterir. Sekant fonksiyonunun grafiği, cosinus fonksiyonunun grafiğinin tersi şeklindedir.
Trigonometrik Özdeşlikler

Trigonometrik özdeşlikler, trigonometrik fonksiyonlar arasındaki matematiksel ilişkilerdir. Bu özdeşlikler, açıların ve kenar uzunluklarının birbirleriyle ilişkisini ifade eder ve matematik, fizik, mühendislik ve diğer bilim dallarında sıklıkla kullanılır.
Birinci tür trigonometrik özdeşlikler, bir trigonometrik fonksiyonunun karesinin diğer iki trigonometrik fonksiyonunun toplamına eşit olduğunu ifade eder. Örneğin, sin²(x) + cos²(x) = 1 özdeşliği, bir açının sinüs fonksiyonunun karesinin, o açının kosinüs fonksiyonunun karesine eklenmesinin her zaman 1’e eşit olduğunu ifade eder.
İkinci tür trigonometrik özdeşlikler, bir trigonometrik fonksiyonunun diğer iki trigonometrik fonksiyonunun oranına eşit olduğunu ifade eder. Örneğin, tan(x) = sin(x) / cos(x) özdeşliği, bir açının tanjant fonksiyonunun, o açının sinüs fonksiyonunun kosinüs fonksiyonuna bölünmesinin her zaman eşit olduğunu ifade eder.
Üçüncü tür trigonometrik özdeşlikler, iki trigonometrik fonksiyonunun çarpımının diğer iki trigonometrik fonksiyona eşit olduğunu ifade eder. Örneğin, sin(x)sin(y) = (1/2)[cos(x-y) – cos(x+y)] özdeşliği, iki açının sinüs fonksiyonlarının çarpımının, bu açıların farkı ve toplamının kosinüs fonksiyonlarına göre hesaplanabileceğini ifade eder.
Trigonometrik özdeşlikler, trigonometrik fonksiyonların arasındaki matematiksel ilişkileri ifade eder ve birçok matematiksel problemin çözümünde kullanılır. Örneğin, bir üçgenin iç açıları ve kenar uzunlukları arasındaki ilişkiyi ifade eden trigonometrik formüller, trigonometrik özdeşliklerin bir örneğidir. Trigonometrik özdeşlikler, ayrıca dairesel trigonometri ve vektör hesaplamaları gibi konularda da sıklıkla kullanılır.
Trigonometrik özdeşlikler, matematiksel olarak kanıtlanabilir ve özdeşlikleri doğrulamak için trigonometrik fonksiyonların grafiklerini kullanabilirsiniz. Bu özdeşlikler, matematiksel problem çözümünde önemli bir araçtır ve birçok matematiksel problemin çözümünde kullanılır.
Kosinüs ve Sinüs Teoremi
Kosinüs Teoremi
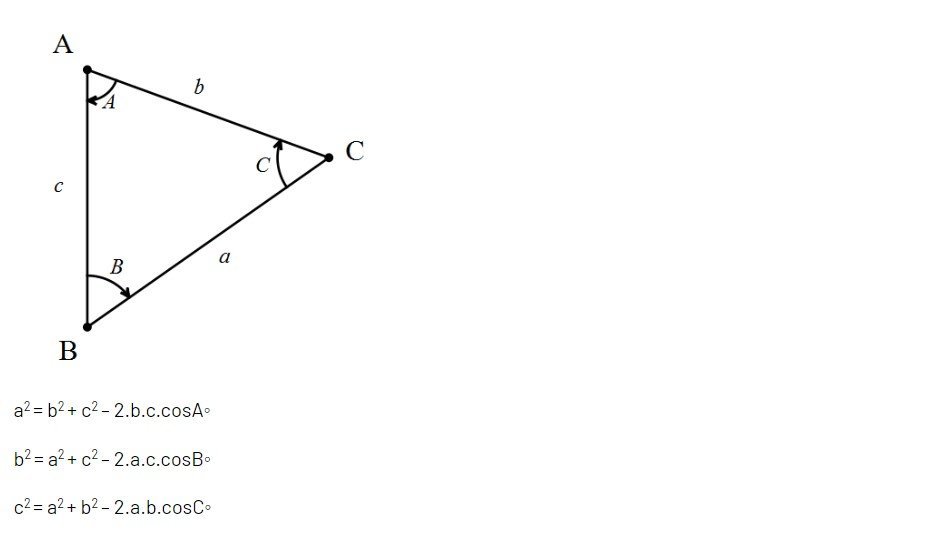
Kosinüs teoremi, bir üçgenin kenarları ve açıları arasındaki ilişkiyi ifade eden bir matematik teoremidir. Bu teorem, üçgenin herhangi bir açısının kosinüs fonksiyonunun diğer iki kenarının uzunluğu ile ilişkisini ifade eder. Kosinüs teoremi, matematik, fizik, mühendislik ve diğer bilim dallarında sıklıkla kullanılır.
Kosinüs teoremi, matematiksel olarak şu şekilde ifade edilir:
c² = a² + b² – 2abcos(C)
Burada, a, b ve c üçgenin kenarlarıdır ve C açısının ölçüsüdür. Bu formül, herhangi bir üçgenin kenar uzunlukları ve açıları arasındaki ilişkiyi ifade eder. Ayrıca, kosinüs teoremi, üçgenin iç açıları ile de ilişkilidir, çünkü üçgenin iç açıları toplamı 180 derecedir.
Kosinüs teoremi, birçok matematiksel problemde kullanılır. Örneğin, bir üçgenin açıları ve kenarları verildiğinde, diğer kenarın uzunluğunu hesaplamak için kosinüs teoremi kullanılabilir. Ayrıca, bir üçgenin yüzey alanını hesaplamak için de kosinüs teoremi kullanılabilir.
Kosinüs teoremi ayrıca vektör hesaplamaları, mekanik, fizik ve diğer bilim dallarında da kullanılır. Örneğin, bir cismi yukarı kaldırmak için gerekli olan gücü hesaplamak için kosinüs teoremi kullanılabilir.
Kosinüs teoremi, matematiksel olarak kanıtlanabilir ve özellikle geometri konusunda temel bir teorem olarak kabul edilir. Kosinüs teoremi, trigonometrik formüllerin temelini oluşturur ve birçok matematiksel problemin çözümünde kullanılır.
Sinüs Teoremi

Sinüs teoremi, bir üçgenin kenarları ve açıları arasındaki ilişkiyi ifade eden bir matematik teoremidir. Bu teorem, üçgenin herhangi bir açısının sinüs fonksiyonunun diğer iki kenarının uzunlukları arasındaki orana eşit olduğunu ifade eder. Sinüs teoremi, matematik, fizik, mühendislik ve diğer bilim dallarında sıklıkla kullanılır.
Sinüs teoremi, matematiksel olarak şu şekilde ifade edilir:
a / sin(A) = b / sin(B) = c / sin(C)
Burada, a, b ve c üçgenin kenarlarıdır ve A, B ve C açılarının ölçüleri sırasıyla karşılık gelen kenarlarının karşısındaki açıların ölçüleridir.
Sinüs teoremi, birçok matematiksel problemin çözümünde kullanılır. Örneğin, bir üçgenin açıları ve kenarları verildiğinde, diğer kenarların uzunluğunu hesaplamak için sinüs teoremi kullanılabilir. Ayrıca, bir üçgenin alanını hesaplamak için de sinüs teoremi kullanılabilir.
Sinüs teoremi, dairesel trigonometri için de önemlidir, çünkü bir üçgenin açıları ve kenarları arasındaki ilişkiyi ifade eder. Bu teorem, trigonometrik fonksiyonların arasındaki ilişkiyi ifade eder ve birçok matematiksel problemin çözümünde kullanılır.
Sinüs teoremi, matematiksel olarak kanıtlanabilir ve özellikle geometri konusunda temel bir teorem olarak kabul edilir. Sinüs teoremi, trigonometrik formüllerin temelini oluşturur ve birçok matematiksel problemin çözümünde kullanılır.
Sonuç olarak, sinüs teoremi, bir üçgenin kenarları ve açıları arasındaki ilişkiyi ifade eden bir matematik teoremidir. Bu teorem, üçgenin herhangi bir açısının sinüs fonksiyonunun diğer iki kenarının uzunlukları arasındaki orana eşit olduğunu ifade eder. Sinüs teoremi, matematiksel olarak kanıtlanabilir ve birçok matematiksel problemin çözümünde kullanılır.