Algoritma Nedir ?

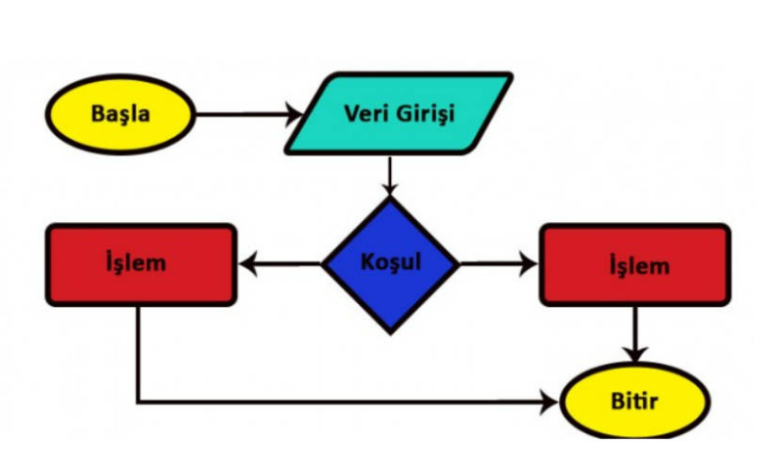
Belirli bir problemi çözmek veya bir işlemi gerçekleştirmek için tasarlanmış bir dizi adım algoritma nedir sorusunun kısa cevabı olacaktır. Bu adımlar, bir programlama dilinde yazılmış bir bilgisayar programında kullanılabilir veya daha genel bir şekilde, bir problemin çözümünü yönlendirmek için kullandığımız bir düşünce sürecini ifade eder.

Algoritma, herhangi bir türden verilerle çalışabilir, ancak genellikle sayısal veya metinsel verilerle ilişkilendirilir. Algoritma tasarlarken, temel amaç, verileri belirli bir sonuca ulaştırmaktır. Algoritmanın etkili bir şekilde çalışması için, adımların tam ve doğru bir şekilde sıralanması gereklidir. Bir algoritma tasarlarken, aşağıdaki adımların izlenmesi önerilir.

Problemin tanımı

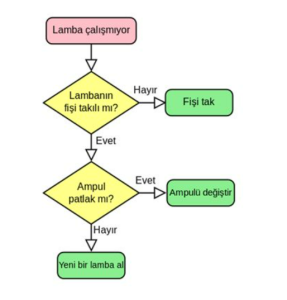
İlk adım, çözmek istediğiniz problemin tanımını yapmaktır. Bu, problemin boyutunu, özelliklerini ve hedeflerini belirlemek için gereklidir. Algoritma tasarımı, bir problemin çözümü için tasarlanmış bir dizi adımdır. Ancak, bir problemi çözmek için bir algoritma tasarlamadan önce, problemi doğru bir şekilde tanımlamak önemlidir. Bir problemi tanımlamak, sorunu belirleyen, çözülmesi gereken sorunun kapsamını belirleyen ve problemin çözümü için neyin gerektiğini netleştiren bir işlemdir. Problemi doğru bir şekilde tanımlamak, algoritma tasarımı için temel bir adımdır. Çünkü, bir problemi yanlış şekilde tanımlamak, algoritmanın yanlış sonuçlar üretmesine neden olabilir.

Bir problemi doğru bir şekilde tanımlamak için; ilk adım, çözmek istediğiniz problemin belirlenmesidir. Bu adım, problemi kapsayan konuyu ve problemin önemini anlamak için gereklidir. İkinci adım, sorunu tanımlamaktır. Bu adım, problemin boyutunu, kapsamını ve sorunu yaratan faktörleri tanımlamak için gereklidir. Üçüncü adım, sorunun çözümü için hedeflerin belirlenmesidir. Bu adım, problemin çözümü için gereken sonuçları belirlemek için gereklidir. Dördüncü adım, sorunun kaynaklarını ve sınırlarını tanımlamaktır. Bu adım, problemin çözümü için kullanılacak kaynakları ve problemin çözümünün mümkün olmadığı durumları belirlemek için gereklidir. Beşinci adım, sorunun çözümü için yöntemlerin belirlenmesidir. Bu adım, sorunu çözmek için kullanılabilecek farklı yöntemleri araştırmak ve analiz etmek için gereklidir. Son adım, sorunun çözümü için en uygun yöntemin seçilmesidir. Bu adım, sorunun çözümü için en uygun yöntemi belirlemek için önceden belirlenen hedefler, kaynaklar ve sınırlar dikkate alınarak yapılır. Problemin doğru bir şekilde tanımlanması, algoritmanın doğru sonuçlar üretmesine yardımcı olur. Ayrıca, problemin doğru bir şekilde tanımlanması, algoritma tasarımının daha etkili ve verimli olmasına yardımcı olur. Doğru problem tanımı, algoritma tasarlama sürecinin daha hızlı ve daha az maliyetli olmasını sağlar. Örneğin, bir web sitesinin yavaş yüklenmesi bir problem olabilir. Ancak, bu problemin nedeni doğru bir şekilde tanımlanmadan, algoritma tasarlamak zor olabilir. Sorun, web sitesinin hızlı yüklenmemesi olarak tanımlanırsa, algoritmanın tasarımı daha doğru ve etkili olacaktır. Problemin doğru bir şekilde tanımlanması, problemin çözümü için gereken kaynakları ve çözüm yöntemlerini belirlemeye de yardımcı olur. Örneğin, bir şirketin müşteri memnuniyeti sorunu varsa, doğru şekilde tanımlanması, müşteri memnuniyetini artırmak için hangi kaynakların ve yöntemlerin kullanılabileceğini belirlemeye yardımcı olacaktır.

Verilerin belirlenmesi

İkinci adım, algoritmanın kullanacağı verilerin belirlenmesidir. Bu, verilerin kaynağı, boyutu ve türü gibi faktörleri içerir. Algoritma tasarlama sürecinde, verilerin doğru bir şekilde belirlenmesi, algoritmanın doğru bir şekilde çalışması için önemlidir. Veriler, algoritmanın kullanacağı girdilerdir ve algoritmanın çözmek istediği problemin niteliğine bağlı olarak değişebilir.

Verilerin belirlenmesi, algoritma tasarımı için temel bir adımdır ve aşağıdaki adımları içerir; ilk adım, verilerin kaynağını belirlemektir. Veriler, bir kullanıcının girdileri olabilir veya bir veri tabanından veya başka bir kaynaktan alınabilir. Verilerin kaynağı, algoritmanın nasıl tasarlandığına ve verilerin ne kadar büyük olduğuna bağlı olarak değişebilir. İkinci adım, verilerin türünü belirlemektir. Veriler, sayılar, metinler, görüntüler veya diğer türlerden oluşabilir. Verilerin türü, algoritmanın nasıl tasarlandığına ve verilerin ne için kullanıldığına bağlı olarak değişebilir. Üçüncü adım, verilerin boyutunu belirlemektir. Verilerin boyutu, algoritmanın verileri ne kadar hızlı işleyebileceğine bağlı olarak önemlidir. Verilerin boyutu, algoritmanın doğru şekilde tasarlanması için dikkate alınması gereken bir faktördür. Dördüncü adım, verilerin biçimini belirlemektir. Veriler, bir matris, bir dizi veya başka bir biçimde düzenlenebilir. Verilerin biçimi, algoritmanın nasıl tasarlandığına ve verilerin işlenmesi için ne kadar hafıza gerektiğine bağlı olarak değişebilir. Beşinci adım, verilerin işlenmesidir. Veriler, algoritmanın tasarımına göre işlenir. Verilerin işlenmesi, algoritmanın doğru şekilde tasarlanması için kritik bir faktördür.

Verilerin doğru şekilde belirlenmesi, algoritmanın doğru şekilde çalışması için kritik bir faktördür. Verilerin doğru bir şekilde belirlenmesi, algoritmanın hızlı ve verimli bir şekilde çalışmasına yardımcı olur. Ayrıca, verilerin doğru bir şekilde belirlenmesi, algoritmanın sonuçları doğru bir şekilde üretmesini sağlar. Örneğin, bir e-ticaret sitesinin algoritması, müşteri siparişleri gibi verileri işleyebilir. Verilerin kaynağı, müşteri siparişleri olabilir. Verilerin türü, sipariş bilgileri, ürünlerin fiyatları, müşteri bilgileri ve benzeri veriler olabilir. Verilerin boyutu, birkaç siparişten binlerce siparişe kadar değişebilir. Verilerin biçimi, siparişlerin bir veri tabanında saklandığı şekilde olabilir. Verilerin işlenmesi, algoritmanın doğru bir şekilde tasarlanması için önemlidir. Örneğin, algoritma, bir müşterinin geçmiş siparişlerine dayanarak öneriler sunabilir veya müşteri davranışlarını analiz ederek hangi ürünlerin en popüler olduğunu belirleyebilir. Başka bir örnek olarak, bir hastalık teşhisi algoritması düşünebiliriz. Verilerin kaynağı, hastanın semptomları olabilir. Verilerin türü, semptomların niteliğine ve şiddetine bağlı olarak değişebilir. Verilerin boyutu, hastanın semptomlarına ve belirtilerine bağlı olarak değişebilir. Verilerin biçimi, semptomların bir dosyada veya bir veri tabanında saklandığı şekilde olabilir. Verilerin işlenmesi, algoritmanın doğru bir şekilde tasarlanması için önemlidir. Örneğin, algoritma, hastanın semptomlarına dayanarak olası teşhisleri belirleyebilir ve gerekli tıbbi testlerin yapılması için öneriler sunabilir.

Adımların belirlenmesi

Üçüncü adım, algoritmanın adımlarını belirlemektir. Bu adımlar, problemin çözümü için gereken tüm işlemleri kapsamalıdır. Algoritma tasarlama, bir problemin çözümü için belirli adımların tasarlanmasıdır. Adımların doğru bir şekilde belirlenmesi, algoritmanın doğru bir şekilde çalışması için hayati önem taşır.

Adımların belirlenmesi, algoritma tasarlamada temel bir adımdır ve aşağıdaki adımları içerir; ilk adım, çözülecek problemi analiz etmektir. Bu adım, problemin kapsamını, nedenlerini ve etkilerini anlamak için gereklidir. İkinci adım, girdilerin belirlenmesidir. Bu adım, problemin çözümü için gereken verileri belirlemek için gereklidir. Girdiler, kullanıcının girdileri, veri tabanlarından veya başka kaynaklardan alınan veriler olabilir. Üçüncü adım, adımların belirlenmesidir. Bu adım, algoritmanın çözmek istediği problemin adımlarını belirlemek için gereklidir. Adımlar, verilerin işlenmesi, hesaplamaların yapılması veya diğer işlemler olabilir. Dördüncü adım, adımların sıralanmasıdır. Bu adım, adımların doğru sırayla gerçekleştirilmesini sağlar. Adımların sıralanması, algoritmanın doğru bir şekilde çalışmasını sağlar. Beşinci adım, algoritmanın tasarımıdır. Bu adım, belirlenen adımların doğru bir şekilde kodlanması ve algoritmanın oluşturulması için gereklidir. Son adım, algoritmanın test edilmesidir. Bu adım, algoritmanın doğru bir şekilde çalıştığından emin olmak için gereklidir. Algoritma, doğru sonuçları üretiyorsa, sorunsuz bir şekilde çalışıyor demektir.

Adımların doğru bir şekilde belirlenmesi, algoritmanın doğru bir şekilde çalışması için kritik bir faktördür. Adımların doğru belirlenmesi, algoritmanın hızlı ve verimli bir şekilde çalışmasına yardımcı olur. Ayrıca, adımların doğru bir şekilde belirlenmesi, algoritmanın sonuçları doğru bir şekilde üretmesini sağlar. Örneğin, bir ödeme sistemi algoritması düşünebiliriz. Girdiler, kullanıcının kredi kartı bilgileri olabilir. Adımlar, kullanıcının bilgilerinin doğru bir şekilde alınması, doğrulanması, ödemesinin yapılması ve son olarak ödemenin tamamlanması olabilir. Adımların sıralanması, doğru bir şekilde sırayla gerçekleştirilmelidir. Algoritma tasarımı, belirlenen adımların doğru bir şekilde kodlanması ve algoritmanın oluşturulması için gereklidir. Algoritmanın test edilmesi, ödeme işlemi tamamlandığında, algoritmanın doğru bir şekilde çalıştığını doğrulamak için gereklidir. Başka bir örnek olarak, bir arama motoru algoritması düşünebiliriz. Girdiler, kullanıcının arama sorgusu olabilir. Adımlar, verilerin taranması, benzer sonuçların sıralanması ve kullanıcıya sunulması olabilir. Adımların sıralanması, doğru bir şekilde sırayla gerçekleştirilmelidir. Algoritma tasarımı, belirlenen adımların doğru bir şekilde kodlanması ve algoritmanın oluşturulması için gereklidir. Algoritmanın test edilmesi, kullanıcının arama sorgusu sonucunda doğru sonuçların üretildiğini doğrulamak için gereklidir.

Adımların sıralanması

Dördüncü adım, belirlenen adımların doğru bir şekilde sıralandığından emin olmaktır. Bu, algoritmanın doğru bir şekilde çalışmasını sağlayacaktır. Algoritma tasarlama sürecinde, adımların doğru bir şekilde sıralanması, algoritmanın doğru bir şekilde çalışması için önemlidir. Adımların sıralanması, algoritmanın girdilerini doğru bir şekilde işlemesini, verileri doğru bir şekilde düzenlemesini ve sonuçları doğru bir şekilde üretmesini sağlar.

Adımların sıralanması, algoritma tasarlamada temel bir adımdır ve aşağıdaki adımları içerir; ilk adım, adımların listelenmesidir. Bu adım, algoritmanın çözmek istediği problemin adımlarını belirlemek için gereklidir. İkinci adım, adımların önceliklendirilmesidir. Bu adım, adımların doğru bir sırayla gerçekleştirilmesini sağlar. Üçüncü adım, adımların tekrarlanmasıdır. Bu adım, adımların doğru sayıda tekrarlanmasını sağlar. Dördüncü adım, adımların koşullu sıralanmasıdır. Bu adım, adımların belirli bir koşula bağlı olarak sıralanmasını sağlar. Beşinci adım, algoritmanın tasarımıdır. Bu adım, belirlenen adımların doğru bir şekilde kodlanması ve algoritmanın oluşturulması için gereklidir. Son adım, algoritmanın test edilmesidir. Bu adım, algoritmanın doğru bir şekilde çalıştığından emin olmak için gereklidir.

Adımların doğru bir şekilde sıralanması, algoritmanın doğru bir şekilde çalışması için kritik bir faktördür. Adımların doğru sıralanması, algoritmanın hızlı ve verimli bir şekilde çalışmasına yardımcı olur. Ayrıca, adımların doğru bir şekilde sıralanması, algoritmanın sonuçları doğru bir şekilde üretmesini sağlar. Örneğin, bir sayıların toplamı algoritması düşünebiliriz. Adımların sıralanması, sayıların doğru bir şekilde alınması, sayıların toplamının hesaplanması ve sonucun kullanıcıya gösterilmesi olabilir. Adımların sıralanması, doğru bir şekilde sırayla gerçekleştirilmelidir. Algoritma tasarımı, belirlenen adımların doğru bir şekilde kodlanması ve algoritmanın oluşturulması için gereklidir. Algoritmanın test edilmesi, sayıların doğru bir şekilde toplandığından emin olmak için gereklidir. Başka bir örnek olarak, bir sıralama algoritması düşünebiliriz. Adımların sıralanması, verilerin doğru bir şekilde sıralanması ve sonucun kullanıcıya gösterilmesi olabilir. Adımların sıralanması, doğru bir şekilde sırayla gerçekleştirilmelidir. Algoritma tasarımı, belirlenen adımların doğru bir şekilde kodlanması ve algoritmanın oluşturulması için gereklidir. Algoritmanın test edilmesi, verilerin doğru bir şekilde sıralandığından emin olmak için gereklidir. Adımların sıralanması, algoritma tasarlamada en önemli adımlardan biridir çünkü adımların doğru bir şekilde sıralanması, algoritmanın doğru bir şekilde çalışmasını sağlar. Adımların sıralanması, belirlenen adımların doğru bir şekilde sırayla gerçekleştirilmesini sağlar. Algoritma tasarımı, belirlenen adımların doğru bir şekilde kodlanması ve algoritmanın oluşturulması için gereklidir. Algoritmanın test edilmesi, algoritmanın doğru bir şekilde çalıştığını doğrulamak için gereklidir.

Adımların uygulanması

Beşinci adım, algoritmanın uygulanmasıdır. Bu, algoritmanın bir programlama dilinde kodlanması veya el ile yapılan hesaplamalarla gerçekleştirilmesi gibi çeşitli şekillerde gerçekleştirilebilir. Algoritma tasarlama sürecinde, adımların doğru bir şekilde uygulanması, algoritmanın doğru bir şekilde çalışması için önemlidir. Adımların uygulanması, algoritmanın girdilerini doğru bir şekilde işlemesini, verileri doğru bir şekilde düzenlemesini ve sonuçları doğru bir şekilde üretmesini sağlar.

Adımların uygulanması, algoritma tasarlamada temel bir adımdır ve aşağıdaki adımları içerir; ilk adım, verilerin işlenmesidir. Bu adım, algoritmanın girdilerini işlemesi ve sonuçları doğru bir şekilde üretmesi için gereklidir. İkinci adım, hesaplamaların yapılmasıdır. Bu adım, verilerin matematiksel veya mantıksal işlemlere tabi tutulması için gereklidir. Üçüncü adım, koşulların değerlendirilmesidir. Bu adım, belirli koşullara bağlı olarak belirli işlemlerin yapılmasını sağlar. Dördüncü adım, döngülerin gerçekleştirilmesidir. Bu adım, belirli işlemlerin belirli koşullar altında belirli sayıda tekrarlanmasını sağlar. Beşinci adım, fonksiyonların kullanımıdır. Bu adım, belirli işlemlerin daha önce tanımlanmış bir fonksiyon tarafından gerçekleştirilmesini sağlar. Son adım, algoritmanın test edilmesidir. Bu adım, algoritmanın doğru bir şekilde çalıştığından emin olmak için gereklidir.

Adımların doğru bir şekilde uygulanması, algoritmanın doğru bir şekilde çalışması için kritik bir faktördür. Adımların doğru bir şekilde uygulanması, algoritmanın hızlı ve verimli bir şekilde çalışmasına yardımcı olur. Ayrıca, adımların doğru bir şekilde uygulanması, algoritmanın sonuçları doğru bir şekilde üretmesini sağlar. Örneğin, bir hesap makinesi algoritması düşünebiliriz. Adımların uygulanması, kullanıcının girdilerinin doğru bir şekilde işlenmesi, hesaplamaların doğru bir şekilde yapılması ve sonucun kullanıcıya gösterilmesi olabilir. Adımların doğru bir şekilde uygulanması, algoritmanın doğru bir şekilde çalışmasını sağlar. Algoritma tasarımı, belirlenen adımların doğru bir şekilde kodlanması ve algoritmanın oluşturulması için gereklidir. Algoritmanın test edilmesi, algoritmanın doğru bir şekilde çalıştığını doğrulamak için gereklidir. Başka bir örnek olarak, bir sıralama algoritması düşünebiliriz. Adımların uygulanması, verilerin doğru bir şekilde sıralanması ve sonucun kullanıcıya gösterilmesi olabilir. Adımların doğru bir şekilde uygulanması, algoritmanın hızlı ve verimli bir şekilde çalışmasını sağlar. Algoritma tasarımı, belirlenen adımların doğru bir şekilde kodlanması ve algoritmanın oluşturulması için gereklidir. Algoritmanın test edilmesi, algoritmanın doğru bir şekilde çalıştığını doğrulamak için gereklidir. Adımların doğru bir şekilde uygulanması, algoritmanın doğru bir şekilde çalışmasını sağlar. Adımların uygulanması, verilerin doğru bir şekilde işlenmesini, hesaplamaların doğru bir şekilde yapılmasını, koşulların doğru bir şekilde değerlendirilmesini, döngülerin doğru bir şekilde gerçekleştirilmesini ve fonksiyonların doğru bir şekilde kullanılmasını sağlar. Algoritmanın test edilmesi, algoritmanın doğru bir şekilde çalıştığını doğrulamak için gereklidir, algoritma nedir.

Test ve Doğrulama

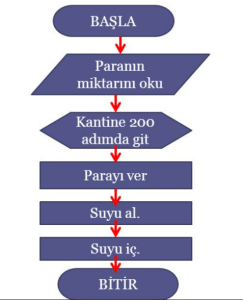
Son adım, algoritmanın test edilmesi ve doğrulanmasıdır. Bu, algoritmanın istenen sonuçları üretip üretmediğini kontrol etmek için yapılan testlerdir. Algoritma tasarlamada, test ve doğrulama süreci algoritmanın doğru bir şekilde çalıştığının doğrulanması için önemlidir. Algoritmanın test edilmesi, algoritmanın doğru bir şekilde çalıştığından emin olmak için gereklidir. Bu süreç, algoritmanın hatalarının tespit edilmesine ve düzeltilmesine yardımcı olur.

Test ve doğrulama süreci, algoritma tasarlama sürecinde temel bir adımdır ve aşağıdaki adımları içerir; ilk adım, test senaryolarının hazırlanmasıdır. Bu adım, algoritmanın test edileceği senaryoların oluşturulması için gereklidir. İkinci adım, algoritmanın uygulanmasıdır. Bu adım, algoritmanın belirlenen test senaryoları üzerinde uygulanması için gereklidir. Üçüncü adım, sonuçların analizidir. Bu adım, algoritmanın sonuçlarının doğru olup olmadığının belirlenmesi için gereklidir. Dördüncü adım, hataların tespiti ve düzeltmedir. Bu adım, algoritmanın hatalarının tespit edilmesi ve düzeltilmesi için gereklidir. Beşinci adım, doğrulamadır. Bu adım, algoritmanın test edildikten sonra doğru bir şekilde çalıştığının doğrulanması için gereklidir, algoritma nedir.

Test ve doğrulama süreci, algoritmanın doğru bir şekilde çalıştığının doğrulanması için kritik bir faktördür. Bu süreç, algoritmanın hatalarının tespit edilmesine ve düzeltilmesine yardımcı olur. Ayrıca, test ve doğrulama süreci, algoritmanın sonuçlarının doğru bir şekilde üretildiğinin belirlenmesini sağlar. Örneğin, bir sıralama algoritması düşünebiliriz. Test senaryolarının hazırlanması, algoritmanın belirli veriler üzerinde doğru bir şekilde çalıştığını doğrulamak için gereklidir. Algoritmanın uygulanması, belirlenen test senaryoları üzerinde algoritmanın çalıştırılması için gereklidir. Sonuçların analizi, algoritmanın doğru bir şekilde sıralama yaptığını doğrulamak için gereklidir. Hataların tespiti ve düzeltme, algoritmanın hatalarının tespit edilmesi ve düzeltilmesi için gereklidir. Doğrulama, algoritmanın test edildikten sonra doğru bir şekilde çalıştığının doğrulanması için gereklidir. Algoritma tasarlama sürecinde test ve doğrulama süreci, algoritmanın doğru bir şekilde çalıştığının doğrulanması için önemlidir. Test ve doğrulama süreci, algoritmanın geliştirilmesi ve hataların tespit edilmesi için bir fırsat sunar. Test ve doğrulama süreci, algoritmanın son kullanıcılar tarafından kullanılabilmesi için gereklidir, algoritma nedir.

Algoritmalar, birçok farklı endüstride kullanılmaktadır. Örneğin, finans sektöründe algoritmalar, hisse senedi fiyatlarını tahmin etmek için kullanılırken, tıp sektöründe algoritmalar, hastalıkların tanısında kullanılabilir. Algoritmaların tasarlanması ve uygulanması, birçok farklı problemi çözmek için kullanışlı bir araçtır. Algoritma tasarlama süreci, daha karmaşık problemlerin bile çözülmesine yardımcı olabilir ve geniş bir uygulama yelpazesine sahiptir. Algoritmaların tasarımı ve uygulanması, birçok endüstriye fayda sağlar ve iş verimliliğini artırır. Algoritmaların tasarımında kullanılan teknikler, problem çözme ve analitik düşünme becerilerini geliştirmeye yardımcı olur. Ayrıca, algoritma tasarımı, birçok farklı programlama dilinde kullanılabilir ve programlama becerilerinin geliştirilmesine de yardımcı olabilir. Algoritmaların gücü, doğru bir şekilde tasarlandığında ve uygulandığında ortaya çıkar. Bu nedenle, algoritmaları tasarlarken, adımların doğru bir şekilde sıralandığından, verilerin doğru bir şekilde kullanıldığından ve algoritmanın doğru bir şekilde uygulandığından emin olmak önemlidir. Algoritmalar, birçok farklı problemi çözmek için kullanışlı bir araçtır. Algoritma tasarlamak, problem çözme ve analitik düşünme becerilerini geliştirmeye yardımcı olurken, programlama becerilerini de geliştirir. Algoritma tasarlama süreci, birçok farklı endüstride kullanılır ve iş verimliliğini artırır, algoritma nedir.

Algoritma Örnekleri

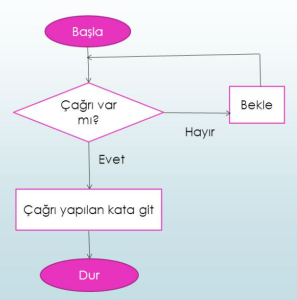
Algoritmalar, birçok farklı konuda kullanılabilirler. Örneğin, matematik, bilgisayar bilimi, finans, fizik ve diğer bilim dallarında kullanılırlar. Aşağıda, farklı alanlarda kullanılan bazı algoritma örnekleri verilmiştir:

• Bubble Sort: Bu algoritma, verileri sıralamak için kullanılır. En küçük veriyi önce sıralar ve ardından diğer verileri sırayla sıralar.
• Dijkstra’s Algorithm: Bu algoritma, ağırlıklı grafiklerde en kısa yol problemi için kullanılır.
• Binary Search: Bu algoritma, bir sıralı dizide verilen bir öğenin konumunu bulmak için kullanılır.
• Quicksort: Bu algoritma, verileri sıralamak için kullanılır. Ayrıca, hızlı bir sıralama algoritması olarak da bilinir.
• Linear Regression: Bu algoritma, veriler arasındaki ilişkiyi analiz etmek ve tahminler yapmak için kullanılır. Özellikle, istatistik ve veri bilimi alanlarında yaygın olarak kullanılır.
• PageRank: Bu algoritma, Google gibi arama motorlarının kullanımında önemli bir rol oynar. Bu algoritma, bir web sayfasının önemini hesaplamak için kullanılır.
• RSA: Bu algoritma, şifreleme ve güvenli iletişim için kullanılır. Özellikle, finans ve bankacılık gibi alanlarda yaygın olarak kullanılır.
• K-Means Clustering: Bu algoritma, veri analizi için kullanılır ve özellikle makine öğrenimi ve veri madenciliği alanlarında yaygın olarak kullanılır.
• Breadth-First Search: Bu algoritma, ağaç veya grafik veri yapılarında kullanılır ve en kısa yol problemi için çözüm sağlar.
• Kruskal’s Algorithm: Bu algoritma, ağırlıklı grafiklerde minimum kapsayan ağacı bulmak için kullanılır.
• A* Algorithm: Bu algoritma, en kısa yol problemlerini çözmek için kullanılır ve özellikle yapay zeka ve oyun geliştirme alanlarında yaygın olarak kullanılır.
• Huffman Encoding: Bu algoritma, verilerin sıkıştırılması için kullanılır. Özellikle, dosya sıkıştırma programlarında yaygın olarak kullanılır.
• Monte Carlo Method: Bu algoritma, rastgele sayı üretme ve olasılıklı hesaplama için kullanılır. Özellikle, matematik, fizik ve finans gibi alanlarda yaygın olarak kullanılır.
• Backpropagation: Bu algoritma, yapay sinir ağlarındaki ağırlıkların optimize edilmesi için kullanılır. Özellikle, derin öğrenme ve yapay zeka alanlarında yaygın olarak kullanılır.
• Euclidean Algorithm: Bu algoritma, en büyük ortak bölen (GCD) hesaplamak için kullanılır. Matematik alanında yaygın olarak kullanılır.
• Floyd-Warshall Algorithm: Bu algoritma, en kısa yol problemleri için kullanılır ve özellikle ağırlıklı grafiklerde kullanılır.
• Bellman-Ford Algorithm: Bu algoritma, ağırlıklı grafiklerde en kısa yol problemleri için kullanılır ve özellikle ağlarda iletişim yönlendirmesi için kullanılır.
• Quickhull: Bu algoritma, çizilen bir kümeye dahil edilen en küçük kapalı çokgeni bulmak için kullanılır. Geometri ve görüntü işleme alanlarında yaygın olarak kullanılır.
• Topological Sort: Bu algoritma, bir yönlü grafikte düğümlerin sıralanması için kullanılır. Özellikle, programlama dillerinde kullanılır.
• Levenshtein Distance: Bu algoritma, iki dizge arasındaki farklılık sayısını bulmak için kullanılır. Özellikle, yazım denetimi ve DNA dizilimi analizi gibi alanlarda yaygın olarak kullanılır.
• Prim’s Algorithm: Bu algoritma, ağırlıklı grafiklerde minimum kapsayan ağaçı bulmak için kullanılır.
• Depth-First Search: Bu algoritma, ağaç veya grafik veri yapılarında kullanılır ve bir çözümün bulunması için tarama yapar.
• Traveling Salesman Problem: Bu algoritma, bir satıcının bir dizi şehri ziyaret etmesi ve en kısa rota üzerinde seyahat etmesi gereken yolculuk planlaması problemi için kullanılır.
• Ford-Fulkerson Algorithm: Bu algoritma, ağırlıklı grafiklerde en büyük akışı bulmak için kullanılır.
• Knapsack Problem: Bu algoritma, sınırlı bir kapasiteye sahip bir çanta içindeki en değerli nesneleri seçmek için kullanılır.
• Merge Sort: Bu algoritma, verileri sıralamak için kullanılır ve hızlı ve verimli bir sıralama algoritmasıdır.
• Bisection Method: Bu algoritma, bir fonksiyonun köklerini bulmak için kullanılır. Özellikle, matematik ve mühendislik alanlarında yaygın olarak kullanılır.
• Newton’s Method: Bu algoritma, bir fonksiyonun köklerini bulmak için kullanılır. Özellikle, matematik, mühendislik ve fizik gibi alanlarda yaygın olarak kullanılır.
• Radix Sort: Bu algoritma, verileri sıralamak için kullanılır ve özellikle büyük veri kümelerinde etkilidir.
• Maximum Subarray Problem: Bu algoritma, bir dizideki ardışık alt dizinin maksimum toplamını bulmak için kullanılır. Özellikle, finans ve ekonomi gibi alanlarda yaygın olarak kullanılır.
• Boyer-Moore Algorithm: Bu algoritma, bir dizgedeki bir alt dizenin konumunu bulmak için kullanılır. Özellikle, yazılım geliştirme ve arama motorları gibi alanlarda yaygın olarak kullanılır.
• Huffman Decoding: Bu algoritma, sıkıştırılmış bir veri kümesini orijinal veri kümesine dönüştürmek için kullanılır.
• Monte Carlo Tree Search: Bu algoritma, oyun ağaçlarındaki en iyi hamleyi bulmak için kullanılır ve özellikle oyun yapay zeka alanında yaygın olarak kullanılır.
• Longest Common Subsequence: Bu algoritma, iki dizge arasındaki en uzun ortak alt diziyi bulmak için kullanılır. Özellikle, biyoinformatik ve yazılım geliştirme alanlarında yaygın olarak kullanılır.
• Aho-Corasick Algorithm: Bu algoritma, bir dizgede birden fazla anahtar kelime aramak için kullanılır. Özellikle, arama motorları ve yazılım geliştirme alanlarında yaygın olarak kullanılır.
• Gauss-Seidel Method: Bu algoritma, bir matrisin doğru bir şekilde çözümü için kullanılır. Özellikle, mühendislik ve fizik gibi alanlarda yaygın olarak kullanılır.
• Dynamic Programming: Bu algoritma, birçok problemi çözmek için kullanılır ve özellikle optimizasyon ve programlama gibi alanlarda yaygın olarak kullanılır.
• Bellman-Held-Karp Algorithm: Bu algoritma, seyahat satıcısı problemi için kullanılır ve bir satıcının bir dizi şehri ziyaret etmesi ve en kısa rota üzerinde seyahat etmesi gereken yolculuk planlaması problemi için çözüm sağlar.
• Karatsuba Algorithm: Bu algoritma, büyük sayılar için çarpma işlemini hızlandırmak için kullanılır. Özellikle, kriptografi ve matematik gibi alanlarda yaygın olarak kullanılır.
• K-nearest Neighbors: Bu algoritma, sınıflandırma ve regresyon problemleri için kullanılır ve özellikle veri madenciliği ve yapay zeka alanlarında yaygın olarak kullanılır.
• RSA Cryptosystem: Bu algoritma, açık anahtarlı şifreleme için kullanılır ve özellikle güvenli iletişim ve kriptografi gibi alanlarda yaygın olarak kullanılır.
• Fisher-Yates Shuffle: Bu algoritma, bir dizinin elemanlarını rastgele karıştırmak için kullanılır. Özellikle, oyun geliştirme ve veri analizi gibi alanlarda yaygın olarak kullanılır.
• Viterbi Algorithm: Bu algoritma, gizli Markov modelleri için kullanılır ve özellikle konuşma tanıma ve doğal dil işleme gibi alanlarda yaygın olarak kullanılır.
• Ford-Johnson Algorithm: Bu algoritma, ağırlıklı grafiklerde en kısa yol problemleri için kullanılır ve özellikle ağlarda iletişim yönlendirmesi için kullanılır.
• Shor’s Algorithm: Bu algoritma, büyük sayıları çarpanlarına ayırmak için kullanılır ve özellikle kriptografi ve matematik gibi alanlarda yaygın olarak kullanılır.
• Hill Cipher: Bu algoritma, şifreleme ve güvenli iletişim için kullanılır ve özellikle kriptografi ve bilgi güvenliği gibi alanlarda yaygın olarak kullanılır.
• Burrows-Wheeler Transform: Bu algoritma, veri sıkıştırma için kullanılır ve özellikle dosya sıkıştırma ve veri iletimi gibi alanlarda yaygın olarak kullanılır.
• Needleman-Wunsch Algorithm: Bu algoritma, iki dizge arasındaki en iyi hizalamayı bulmak için kullanılır ve özellikle biyoinformatik ve genetik gibi alanlarda yaygın olarak kullanılır.
• Hopfield Network: Bu algoritma, yapay sinir ağları için kullanılır ve özellikle derin öğrenme ve yapay zeka gibi alanlarda yaygın olarak kullanılır.
• Hough Transform: Bu algoritma, nesne algılama ve tanıma için kullanılır ve özellikle görüntü işleme ve robotik gibi alanlarda yaygın olarak kullanılır.
• Bloom Filter: Bu algoritma, bir elemanın bir kümeye ait olup olmadığını hızlı bir şekilde kontrol etmek için kullanılır. Özellikle, veritabanı yönetimi ve ağ trafiği analizi gibi alanlarda yaygın olarak kullanılır.
• Apriori Algorithm: Bu algoritma, veri madenciliği ve makine öğrenimi için kullanılır ve özellikle bir dizi madde satışı veya tüketici davranışlarının analizi gibi alanlarda yaygın olarak kullanılır.
• Kruskal’s Algorithm: Bu algoritma, minimum kapsayan ağaç problemleri için kullanılır ve özellikle ağ tasarımı ve ulaşım mühendisliği gibi alanlarda yaygın olarak kullanılır.
• Canny Edge Detection: Bu algoritma, görüntü işleme için kullanılır ve özellikle nesne tanıma ve robotik görme gibi alanlarda yaygın olarak kullanılır.
• Genetic Algorithm: Bu algoritma, optimizasyon problemleri için kullanılır ve özellikle mühendislik, tasarım ve yapay zeka gibi alanlarda yaygın olarak kullanılır.
• Smith-Waterman Algorithm: Bu algoritma, iki dizge arasındaki en iyi hizalamayı bulmak için kullanılır ve özellikle biyoinformatik ve genetik gibi alanlarda yaygın olarak kullanılır.
• Lempel-Ziv-Welch Algorithm: Bu algoritma, veri sıkıştırma için kullanılır ve özellikle dosya sıkıştırma ve veri iletimi gibi alanlarda yaygın olarak kullanılır.
• Expectation-Maximization Algorithm: Bu algoritma, istatistiksel verilerin analizi ve parametre tahmini için kullanılır ve özellikle veri madenciliği ve yapay zeka gibi alanlarda yaygın olarak kullanılır.
• Dijkstra’s Algorithm: Bu algoritma, en kısa yol problemleri için kullanılır ve özellikle ağ yönlendirmesi, harita rotalama ve seyahat planlaması gibi alanlarda yaygın olarak kullanılır.
• Dempster-Shafer Theory: Bu algoritma, belirsizlik altında sonuçların analizi ve karar verme için kullanılır ve özellikle yapay zeka ve nesne tanıma gibi alanlarda yaygın olarak kullanılır.
• Fisher’s Linear Discriminant: Bu algoritma, sınıflandırma ve özellik seçimi için kullanılır ve özellikle görüntü işleme ve biyomedikal mühendisliği gibi alanlarda yaygın olarak kullanılır.
• Levenshtein Distance: Bu algoritma, iki dizge arasındaki mesafeyi hesaplamak için kullanılır ve özellikle doğal dil işleme ve veri tabanları gibi alanlarda yaygın olarak kullanılır.
• Boyer-Moore-Horspool Algorithm: Bu algoritma, bir dizgedeki bir alt dizenin konumunu bulmak için kullanılır ve özellikle yazılım geliştirme ve arama motorları gibi alanlarda yaygın olarak kullanılır.
• Fast Fourier Transform: Bu algoritma, sinyal işleme ve spektral analiz için kullanılır ve özellikle mühendislik, matematik ve fizik gibi alanlarda yaygın olarak kullanılır.
• K-Means Clustering: Bu algoritma, veri kümelemesi için kullanılır ve özellikle veri madenciliği, yapay zeka ve görüntü işleme gibi alanlarda yaygın olarak kullanılır.
• Gale-Shapley Algorithm: Bu algoritma, stabil evlilik problemleri için kullanılır ve özellikle ekonomi, sosyoloji ve işletme gibi alanlarda yaygın olarak kullanılır.
• Backpropagation: Bu algoritma, yapay sinir ağlarında kullanılır ve özellikle derin öğrenme, görüntü işleme ve doğal dil işleme gibi alanlarda yaygın olarak kullanılır.
• Principal Component Analysis: Bu algoritma, veri boyut azaltma ve özellik çıkarımı için kullanılır ve özellikle mühendislik, bilgisayar görüşü ve veri madenciliği gibi alanlarda yaygın olarak kullanılır.
• Longest Increasing Subsequence: Bu algoritma, bir dizideki ardışık alt dizilerin en uzun artan alt dizisini bulmak için kullanılır ve özellikle veri analizi ve sıralama gibi alanlarda yaygın olarak kullanılır.
• Gale-Nikaido-Debreu Theorem: Bu algoritma, Walras genel dengesi teorisinde kullanılır ve özellikle ekonomi, matematik ve işletme gibi alanlarda yaygın olarak kullanılır.
• PageRank Algorithm: Bu algoritma, web sayfalarının önemini belirlemek için kullanılır ve özellikle arama motorları ve internet trafiği gibi alanlarda yaygın olarak kullanılır.
• A* Algorithm: Bu algoritma, en kısa yol problemleri için kullanılır ve özellikle yapay zeka, robotik ve oyun geliştirme gibi alanlarda yaygın olarak kullanılır.
• Naive Bayes Classifier: Bu algoritma, sınıflandırma için kullanılır ve özellikle doğal dil işleme ve veri madenciliği gibi alanlarda yaygın olarak kullanılır.
• Smith Normal Form Algorithm: Bu algoritma, tamsayı matrislerinin özelliklerini hesaplamak için kullanılır ve özellikle matematik ve fizik gibi alanlarda yaygın olarak kullanılır.
• Bellman-Ford Algorithm: Bu algoritma, ağırlıklı grafiklerde en kısa yol problemleri için kullanılır ve özellikle ağ tasarımı ve ulaşım mühendisliği gibi alanlarda yaygın olarak kullanılır.
• QuickSort: Bu algoritma, bir diziyi hızlı bir şekilde sıralamak için kullanılır ve özellikle veri tabanları ve bilgisayar programlama gibi alanlarda yaygın olarak kullanılır.
• Radix Sort: Bu algoritma, sıralama için kullanılır ve özellikle büyük veri kütleleriyle çalışan uygulamalar gibi alanlarda yaygın olarak kullanılır.
• Traveling Salesman Problem: Bu algoritma, en kısa yol problemleri için kullanılır ve özellikle lojistik, ulaşım ve seyahat gibi alanlarda yaygın olarak kullanılır.
• Euclidean Algorithm: Bu algoritma, en büyük ortak böleni hesaplamak için kullanılır ve özellikle matematik, kriptografi ve veri güvenliği gibi alanlarda yaygın olarak kullanılır.
• Damerau-Levenshtein Distance: Bu algoritma, iki dizge arasındaki mesafeyi hesaplamak için kullanılır ve özellikle yazılım geliştirme, doğal dil işleme ve veri tabanları gibi alanlarda yaygın olarak kullanılır.
• SHA-256: Bu algoritma, güvenli bir şekilde mesaj özeti oluşturmak için kullanılır ve özellikle veri güvenliği ve kriptografi gibi alanlarda yaygın olarak kullanılır.
• Rabin-Karp Algorithm: Bu algoritma, bir dizgedeki bir alt dizenin konumunu bulmak için kullanılır ve özellikle yazılım geliştirme ve veri tabanları gibi alanlarda yaygın olarak kullanılır.
• Boyer-Moore Algorithm: Bu algoritma, bir dizgedeki bir alt dizenin konumunu bulmak için kullanılır ve özellikle yazılım geliştirme ve arama motorları gibi alanlarda yaygın olarak kullanılır.
• Huffman Coding: Bu algoritma, veri sıkıştırma için kullanılır ve özellikle dosya sıkıştırma ve veri iletimi gibi alanlarda yaygın olarak kullanılır.
• Floyd-Warshall Algorithm: Bu algoritma, tüm çiftler en kısa yol problemleri için kullanılır ve özellikle ağ tasarımı ve ulaşım mühendisliği gibi alanlarda yaygın olarak kullanılır.
• Knuth-Morris-Pratt Algorithm: Bu algoritma, bir dizgedeki bir alt dizenin konumunu bulmak için kullanılır ve özellikle yazılım geliştirme ve veri tabanları gibi alanlarda yaygın olarak kullanılır.
• Needleman-Wunsch Algorithm: Bu algoritma, iki dizge arasındaki en iyi hizalamayı bulmak için kullanılır ve özellikle biyoinformatik ve genetik gibi alanlarda yaygın olarak kullanılır.
• Gale-Shapley Algorithm: Bu algoritma, stabil evlilik problemleri için kullanılır ve özellikle ekonomi, sosyoloji ve işletme gibi alanlarda yaygın olarak kullanılır.
• Hopcroft-Karp Algorithm: Bu algoritma, eşleştirme problemleri için kullanılır ve özellikle bilgisayar ağları ve veri tabanları gibi alanlarda yaygın olarak kullanılır.
• Rete Algorithm: Bu algoritma, yapay zeka ve uzman sistemlerde kullanılır ve özellikle karar destek sistemleri ve diğer uzman sistem uygulamalarında yaygın olarak kullanılır.
• Prim’s Algorithm: Bu algoritma, ağaç oluşturma problemleri için kullanılır ve özellikle mühendislik, bilgisayar ağları ve veri madenciliği gibi alanlarda yaygın olarak kullanılır.
• Tarjan’s Algorithm: Bu algoritma, grafiklerdeki güçlü bağlantı bileşenlerini bulmak için kullanılır ve özellikle mühendislik, bilgisayar ağları ve veri madenciliği gibi alanlarda yaygın olarak kullanılır.
• Edmonds-Karp Algorithm: Bu algoritma, akış ağırlıklı grafiklerde en büyük akış problemleri için kullanılır ve özellikle ağ tasarımı ve ulaşım mühendisliği gibi alanlarda yaygın olarak kullanılır.
• Hungarian Algorithm: Bu algoritma, eşleştirme problemleri için kullanılır ve özellikle üretim planlaması ve lojistik gibi alanlarda yaygın olarak kullanılır.
• Viterbi Algorithm: Bu algoritma, gizli Markov modellerinde en olası durum dizilimini hesaplamak için kullanılır ve özellikle doğal dil işleme ve konuşma tanıma gibi alanlarda yaygın olarak kullanılır.
• Douglas-Peucker Algorithm: Bu algoritma, bir çizginin düzleştirilmesi ve sadeleştirilmesi için kullanılır ve özellikle haritalama ve diğer görselleştirme uygulamalarında yaygın olarak kullanılır.
• Gaussian Elimination: Bu algoritma, tamsayı matrislerinin özelliklerini hesaplamak için kullanılır ve özellikle matematik ve fizik gibi alanlarda yaygın olarak kullanılır.
• Apriori Algorithm: Bu algoritma, veri madenciliği için kullanılır ve özellikle perakende ve pazarlama gibi alanlarda yaygın olarak kullanılır.
• Kruskal’s Algorithm: Bu algoritma, ağaç oluşturma problemleri için kullanılır ve özellikle mühendislik, bilgisayar ağları ve veri madenciliği gibi alanlarda yaygın olarak kullanılır.
• Genetic Algorithm: Bu algoritma, optimizasyon problemleri için kullanılır ve özellikle yapay zeka, mühendislik ve bilgisayar bilimi gibi alanlarda yaygın olarak kullanılır.

Bu algoritma örnekleri, algoritmaların farklı alanlarda nasıl kullanılabileceğine dair birkaç örnektir. Algoritmalar, birçok farklı problemi çözmek için kullanılabilir ve sıklıkla kullanılır. Yeni problemlerle karşılaşıldığında, var olan algoritmaları değiştirmek veya yeni algoritmalar geliştirmek mümkündür, algoritma nedir.

Algoritma Analizi

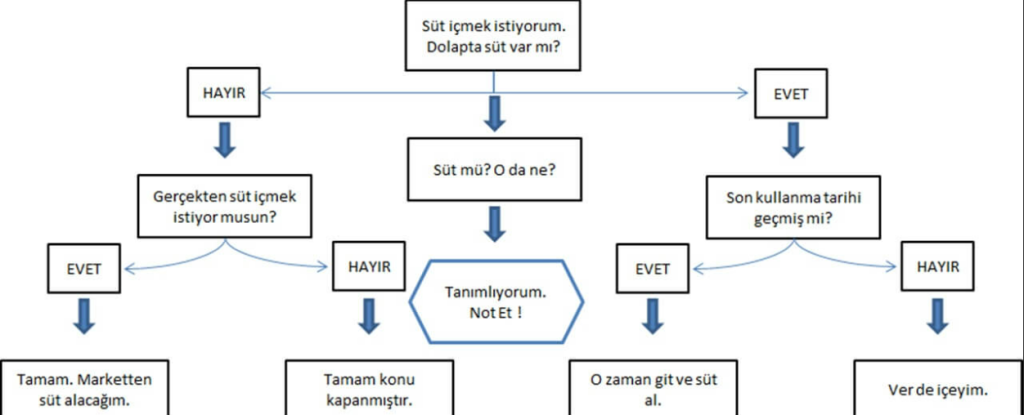
Algoritma Analizi Nedir?

Algoritma analizi, bir algoritmanın performansını ve verimliliğini incelemek için kullanılan bir matematiksel yöntemdir. Bu analiz, bir algoritmanın çalışma süresinin ve kullanılan bellek miktarının tahmin edilmesine yardımcı olur. Bu sayede, algoritmaların ne kadar verimli olduğu, ne kadar işlem gücüne ihtiyaç duydukları ve ne kadar hafıza kullanacakları tahmin edilebilir.

Algoritma Analizinin Önemi

Algoritma analizi, bir algoritmanın verimliği hakkında bilgi verir. Bu bilgi, bir algoritmanın uygulama alanlarının belirlenmesine, programlama dillerinin seçimine ve bilgisayar donanımlarının seçimine yardımcı olur. Ayrıca, algoritma analizi, bir algoritmanın performansını artırmak için yapılacak değişikliklerin belirlenmesinde de kullanılır.

Algoritma Analizi Yöntemleri

Algoritma analizi, çeşitli yöntemler kullanılarak yapılabilir. Bunlar arasında zamana dayalı analiz, bellek kullanımı analizi, işlemci kullanımı analizi, hesaplama yoğunluğu analizi ve uzay-yoğunluk analizi yer alır.

Zamana Dayalı Analiz: Zamana dayalı analiz, bir algoritmanın çalışma süresini tahmin etmek için kullanılır. Bu analiz, bir algoritmanın girdi boyutunun artmasıyla birlikte çalışma süresinin nasıl değişeceğini gösterir.

Bellek Kullanımı Analizi: Bellek kullanımı analizi, bir algoritmanın ne kadar bellek kullanacağını tahmin etmek için kullanılır. Bu analiz, bir algoritmanın bellek kullanımının girdi boyutuna göre nasıl değiştiğini gösterir.

İşlemci Kullanımı Analizi: İşlemci kullanımı analizi, bir algoritmanın işlemci kullanımını tahmin etmek için kullanılır. Bu analiz, bir algoritmanın işlemci kullanımının girdi boyutuna göre nasıl değiştiğini gösterir.

Hesaplama Yoğunluğu Analizi: Hesaplama yoğunluğu analizi, bir algoritmanın hesaplama yoğunluğunu tahmin etmek için kullanılır. Bu analiz, bir algoritmanın işlemci kullanımının yanı sıra hesaplama yoğunluğunu da dikkate alır.

Uzay-Yoğunluk Analizi: Uzay-yoğunluk analizi, bir algoritmanın uzay kullanımını tahmin etmek için kullanılır. Bu analiz, bir algoritmanın kullanacağı uzayın girdi boyutuna göre nasıl değiştiğini gösterir.

Algoritma Analizi Örnekleri

Örnek olarak, bir sıralama algoritması olan Bubble Sort algoritmasının zamana dayalı analizi yapılabilir. Bubble Sort algoritması, bir dizi elemanı küçükten büyüğe veya büyükten küçüğe sıralamak için kullanılır. Bu algoritmanın çalışma süresi, girdi boyutunun kare köküyle orantılıdır.

Örneğin, bir dizinin Bubble Sort algoritmasıyla sıralanması için 100 elemanının olduğunu varsayalım. Bu durumda, Bubble Sort algoritmasının çalışma süresi, 100^2 = 10.000 işlem adımına eşit olacaktır. Aynı şekilde, 1.000 elemanlı bir dizinin sıralanması için Bubble Sort algoritmasının çalışma süresi 1.000^2 = 1.000.000 işlem adımına eşit olacaktır. Bu örnek, zamana dayalı analiz yönteminin nasıl uygulandığını gösterir. Bu yöntem, bir algoritmanın performansının tahmin edilmesi için önemlidir ve algoritmaların verimli bir şekilde tasarlanmasına yardımcı olur, algoritma nedir.

Algoritma Şekilleri

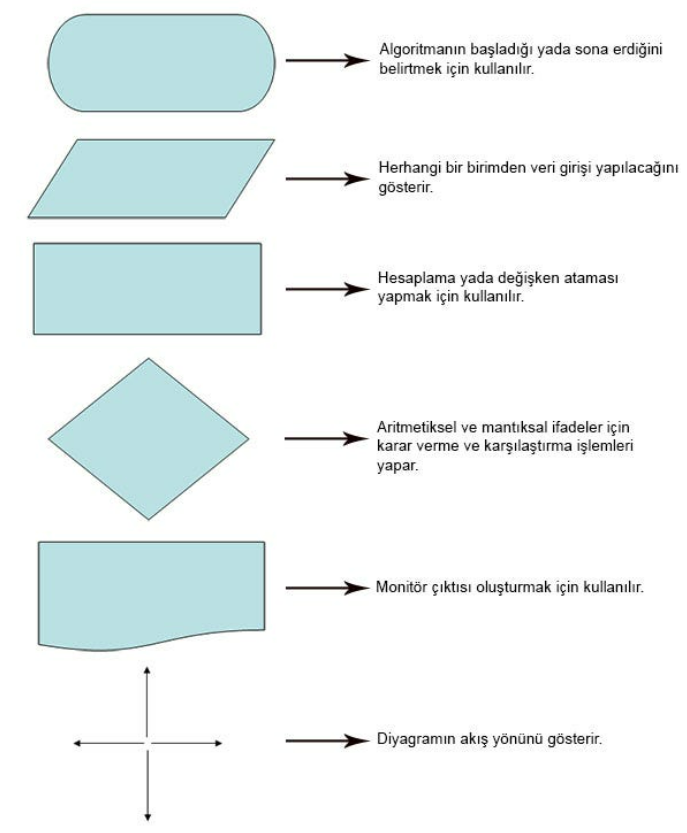
Algoritmalar, çeşitli şekillerde gösterilebilir, algoritma nedir. Bu şekiller, bir algoritmanın anlaşılmasını kolaylaştırır ve görsel olarak gösterir. En yaygın kullanılan algoritma şekilleri şunlardır:

Akış Şeması

Akış şeması, algoritmaları görsel olarak gösteren en popüler şekillerden biridir. Bu şema, dikdörtgen, elips, rombus, oklar ve diğer şekillerden oluşur. Dikdörtgen, işlemi temsil ederken, elips, başlangıç veya bitiş noktasını temsil eder. Oklar, işlemlerin veya kontrol yapılarının akışını gösterir.

Yapısal Şema

Yapısal şema, bir algoritmanın mantığını açıklamak için kullanılan bir şekildir. Bu şema, bloklar, çizgiler, simgeler ve metinlerden oluşur. Bloklar, işlemleri veya işlem gruplarını, çizgiler, bu işlemlerin birbirine bağlanmasını, simgeler, işlemlerin türünü ve metinler, açıklamaları temsil eder.

Nassi-Shneiderman Şeması

Bu şema, akış şemasına benzerdir ancak daha modern bir yaklaşımdır. Bu şema, işlem bloklarını, karar bloklarını ve döngü bloklarını içerir. İşlem blokları dikdörtgen şeklindedir, karar blokları rombus şeklindedir ve döngü blokları ise elips şeklindedir.

Pseudocode

Pseudocode, bir algoritmanın metin tabanlı bir gösterimidir. Bu gösterim, programlama diline özgü değildir ve herhangi bir programlama dilinde uygulanabilir. Pseudocode, algoritmanın adımlarını ve mantığını açıklayan bir yazılım kodu gibi yazılır.

UML Şeması

UML, Unified Modeling Language (Birleşik Modelleme Dili) kısaltmasıdır. Bu şema, nesne yönelimli programlama için kullanılır ve sınıf diyagramları, nesne diyagramları ve aktivite diyagramları gibi farklı diyagram türlerini içerir.

Algoritma Şekilleri Örnekleri

Örneğin, Bubble Sort algoritmasının akış şeması şu şekilde gösterilebilir:

[Elips] Başla

[Dikdörtgen] Dizi elemanlarını al

[Dikdörtgen] Diziyi sırala

[Dikdörtgen] Sıralanmış diziyi göster

[Elips] Bitir

Benzer şekilde, aynı algoritmanın Nassi-Shneiderman şeması şu şekilde olabilir:

[Elips] Başla

[Dikdörtgen] Dizi elemanlarını al

[Döngü] Her i=1’den n-1’e kadar

[Rombus] Eğer dizi[i]>d

[Dikdörtgen] Dizi[i] ile dizi[i+1]’i yer değiştir

[Döngü] Bitir

[Dikdörtgen] Sıralanmış diziyi göster

[Elips] Bitir

Bubble Sort algoritmasının pseudocode gösterimi ise şöyle olabilir:

1. Başla
2. Dizi elemanlarını al
3. n = dizinin uzunluğu
4. Döngü i=0’dan n-1’e kadar
5. Döngü j=0’dan n-i-1’e kadar
6. Eğer(dizi[j] > dizi[j+1])
7. dizi[j] ile dizi[j+1]’i yer değiştir
8. Eğer Sonu
9. Döngü Bitir
10. Döngü Bitir
11. Sıralanmış diziyi göster
12. Bitir

Algoritma şekilleri, bir algoritmanın görsel olarak ifade edilmesine yardımcı olan farklı yöntemlerdir. Akış şeması, yapısal şema, Nassi-Shneiderman şeması, pseudocode ve UML şeması, en yaygın kullanılan algoritma şekilleridir. Bu şekiller, bir algoritmanın anlaşılmasını kolaylaştırır ve görsel bir tanım sağlar, algoritma nedir.