Çembersel Hareket Nedir ?

Çembersel hareket nedir, bir dönme hareketidir ve genellikle fizik, mühendislik ve astronomi gibi alanlarda incelenir.
Çembersel hareket, bir cismin sabit bir merkez etrafında dönme hareketidir. Bu hareketin en temel özelliği, dönme hareketinin düzlemde gerçekleşmesidir. Çembersel hareketin matematiksel ifadesi, çemberdeki açısal hız ve açısal ivme ile ifade edilir. Açısal hız, bir cismin birim zamanda döndüğü açı miktarıdır ve radyan/saniye cinsinden ölçülür. Açısal ivme ise birim zamanda açısal hızın ne kadar arttığıdır ve radyan/saniye^2 cinsinden ölçülür. Çembersel hareket, birçok farklı uygulama alanında kullanılır. Örneğin, araba lastikleri, rulmanlar, turbojet motorları ve dönme hareketi kullanan birçok makinelerde çembersel hareket prensibi kullanılır. Aynı zamanda, astronomi alanında da gezegenlerin ve yıldızların hareketi çembersel hareket prensipleri kullanılarak incelenir. Çembersel hareket hesaplamaları, trigonometrik fonksiyonlar ve diferansiyel denklemler gibi matematiksel kavramları içerir. Bu hesaplamalar, özellikle mühendislik ve fizik alanında çalışanlar tarafından sıklıkla kullanılır. Çembersel hareket, hareket halindeki bir cismin hızı, ivmesi ve kuvveti gibi fiziksel özelliklerinin belirlenmesi için önemlidir. Bu özellikler, özellikle mühendislik alanında tasarımların yapılması ve bu tasarımların doğruluğunun kontrol edilmesi için kullanılır. Çembersel hareketin matematiksel formülleri, çemberin yarıçapı, açısal hızı ve açısal ivmesi gibi değişkenlere dayanır. Örneğin, bir çemberdeki hareketin hızı, çemberin yarıçapı ve açısal hızın çarpımı ile belirlenir. Benzer şekilde, açısal ivme, açısal hızın zamana göre türevi olarak belirlenir. Gerçek hayatta, birçok cihaz ve araç, çembersel hareket prensiplerine dayanır. Örneğin, araba lastikleri çembersel hareket kullanarak yere tutunur. Turbojet motorları, fanların çembersel hareketi sayesinde hava emer ve itici güç oluşturur. Bu gibi durumlarda, çembersel hareketin hesaplamaları, tasarımların doğruluğunu kontrol etmek için kullanılır. Çembersel hareket, mühendislik, fizik ve astronomi gibi alanlarda sıklıkla kullanılan bir prensiptir. Çembersel hareketin hesaplamaları, birçok tasarımın doğruluğunu kontrol etmek ve özelliklerini belirlemek için kullanılır. Aynı zamanda, çembersel hareket prensipleri, gerçek hayatta birçok cihaz ve araçta kullanılır.
Düzgün Çembersel Hareket

Düzgün çembersel hareket, bir cismi sabit bir merkez etrafında düzgün bir şekilde döndüren harekettir. Bu hareket, matematiksel olarak tanımlanabilir ve birçok uygulama alanında kullanılır.
Düzgün çembersel hareket, sabit bir merkez etrafında eşit açısal hızda dönme hareketidir. Bu hareket, bir çemberin tamamını eşit sürelerde dolaşan bir cisim tarafından gerçekleştirilebilir. Düzgün çembersel hareket, düzlemde gerçekleşen bir harekettir ve hareketin matematiksel ifadesi, açısal hız ve çemberin yarıçapı gibi değişkenlere dayanır. Düzgün çembersel hareket, birçok uygulama alanında kullanılır. Örneğin, birçok makinelerde kullanılan rulmanlar ve kayış kasnakları, düzgün çembersel hareket prensiplerine dayanır. Ayrıca, döner trafik lambaları ve dönme hareketli kalemler gibi birçok ürün de düzgün çembersel hareket prensipleri kullanılarak tasarlanır. Düzgün çembersel hareket hesaplamaları, trigonometrik fonksiyonlar ve vektörler gibi matematiksel kavramları içerir. Açısal hız, açısal ivme ve merkezcil kuvvet gibi çeşitli fiziksel özellikler de hesaplanabilir. Bu hesaplamalar, özellikle mühendislik ve fizik alanında çalışanlar tarafından sıklıkla kullanılır. Düzgün çembersel hareketin önemli bir özelliği, cismin merkeze doğru yönelen bir merkezcil kuvvetin oluşmasıdır. Bu kuvvet, cismin yönünü merkeze doğru çevirir ve hareketin devam etmesini sağlar. Bu kuvvet, düzgün çembersel hareketin matematiksel hesaplamalarında da kullanılır. Düzgün çembersel hareket, sabit bir merkez etrafında düzgün bir şekilde dönen bir cisim tarafından gerçekleştirilen bir harekettir. Bu hareketin matematiksel hesaplamaları, trigonometrik fonksiyonlar ve vektörler gibi matematiksel kavramları içerir. Düzgün çembersel hareket, birçok uygulama alanında kullanılan bir prensiptir ve mühendislik ve fizik alanında çalışanlar tarafından sıklıkla kullanılır.
Açısal Hız Ve Merkezcil İvme
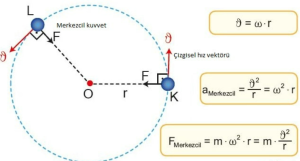
Açısal hız ve merkezcil ivme, çembersel hareketin temel özellikleridir ve fizik, mühendislik ve astronomi gibi birçok alanda incelenir.
Açısal hız, bir cismin birim zamanda döndüğü açı miktarıdır ve radyan/saniye cinsinden ölçülür. Bir cisim, sabit bir merkez etrafında dönme hareketi yaparken, açısal hızı sabit kalır. Açısal hızın matematiksel ifadesi, dönüş açısının zamana göre türevi olarak verilir. Açısal hız, çembersel hareketin matematiksel hesaplamalarında önemli bir özelliktir. Merkezcil ivme, bir cismin sabit bir merkez etrafındaki dönme hareketinde, merkeze doğru yönelen ivmedir. Bu ivme, cismin dönme hareketi sırasında yön değiştirmesini sağlar ve hareketin devam etmesini sağlar. Merkezcil ivmenin matematiksel ifadesi, açısal hızın karesinin çemberin yarıçapına bölünmesiyle elde edilir. Merkezcil ivme, çembersel hareketin matematiksel hesaplamalarında önemli bir özelliktir. Açısal hız ve merkezcil ivme, birçok uygulama alanında kullanılır. Örneğin, araba lastikleri, rulmanlar ve turbojet motorları gibi birçok cihaz ve araç, çembersel hareket prensiplerine dayanır. Açısal hız ve merkezcil ivmenin hesaplamaları, özellikle mühendislik ve fizik alanında tasarımların doğruluğunun kontrol edilmesi için kullanılır. Ayrıca, astronomi alanında da açısal hız ve merkezcil ivme önemli bir rol oynar. Gezegenlerin ve yıldızların hareketi, açısal hız ve merkezcil ivme hesaplamaları kullanılarak incelenir. Bu hesaplamalar, uzayda seyahat eden araçların da hareketini kontrol etmek için kullanılabilir. Açısal hız ve merkezcil ivme, çembersel hareketin önemli özellikleridir. Bu özellikler, özellikle mühendislik, fizik ve astronomi alanlarında kullanılır. Açısal hız ve merkezcil ivmenin hesaplamaları, tasarımların doğruluğunun kontrol edilmesi için önemlidir ve gerçek hayatta birçok cihaz ve araçta kullanılır.
Çembersel Hareket Formülleri
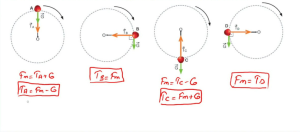
Çembersel hareket problemleri, fizik ve mühendislik alanında sıklıkla karşılaşılan problemlerdir. Bu problemler genellikle bir cismin sabit bir merkez etrafında döndüğü durumlarda ortaya çıkar.
Çembersel hareket problemleri için kullanılan en temel formüllerden biri açısal hız formülüdür. Açısal hız, bir cismin birim zamanda döndüğü açı miktarıdır ve radyan/saniye cinsinden ölçülür. Açısal hız formülü, w = θ/t şeklinde ifade edilir, burada w açısal hız, θ ise dönüş açısı, t ise zaman dilimidir. Çembersel hareket problemlerinde kullanılan bir diğer formül açısal ivme formülüdür. Açısal ivme, birim zamanda açısal hızın ne kadar arttığıdır ve radyan/saniye^2 cinsinden ölçülür. Açısal ivme formülü, α = dw/dt şeklinde ifade edilir, burada α açısal ivme, w açısal hız ve t zaman dilimidir. Çembersel hareket problemleri için kullanılan bir başka formül merkezcil ivme formülüdür. Merkezcil ivme, bir cismin dönme hareketi sırasında merkeze doğru yönelen ivmedir. Bu ivme, cismin yön değiştirmesini sağlar ve hareketin devam etmesini sağlar. Merkezcil ivme formülü, a = w^2*r şeklinde ifade edilir, burada a merkezcil ivme, w açısal hız ve r çemberin yarıçapıdır. Çembersel hareket problemleri için kullanılan diğer formüller arasında, çemberin çevresi, alanı, çapı, yarıçapı ve uzunluğu gibi özellikleri hesaplamak için kullanılan formüller yer alır. Örneğin, bir çemberin alanı A = πr^2 şeklinde hesaplanır. Çemberin çevresi ise C = 2π*r şeklinde hesaplanır. Çembersel hareket problemlerinde kullanılan birçok formül vardır. Bu formüller, açısal hız, açısal ivme, merkezcil ivme, çemberin özellikleri gibi konuları hesaplamak için kullanılır. Çembersel hareket problemlerinin çözümünde bu formüllerin doğru bir şekilde kullanılması, tasarımın doğruluğunu kontrol etmek ve problemin çözümünü kolaylaştırmak için önemlidir.
- Açısal hız formülü: w = θ/t
Bu formülde, w açısal hızı, θ dönüş açısını ve t zamanı temsil eder.
- Açısal ivme formülü: α = dw/dt
Bu formülde, α açısal ivmeyi, w açısal hızı ve t zamanı temsil eder.
- Merkezcil ivme formülü: a = w^2*r
Bu formülde, a merkezcil ivmeyi, w açısal hızı ve r çemberin yarıçapını temsil eder.
- Çemberin çevresi formülü: C = 2πr
Bu formülde, C çemberin çevresini ve r çemberin yarıçapını temsil eder.
- Çemberin alanı formülü: A = π*r^2
Bu formülde, A çemberin alanını ve r çemberin yarıçapını temsil eder.
- Moment formülü: I = m*r^2
Bu formülde, I momenti, m cismin kütlesini ve r çemberin yarıçapını temsil eder.
- Sürtünme kuvveti formülü: F = μ*N
Bu formülde, F sürtünme kuvvetini, μ sürtünme katsayısını ve N normal kuvvetini temsil eder.
Çembersel Hareket Çıkmış Sorular

Çembersel hareket nedir konusuyla ilgili sınavlarda çıkabilecek bazı soru örnekleri şöyledir:
- Bir araba, sabit bir merkez etrafında dönerek hareket ediyor. Arabanın açısal hızı 2 rad/s ve dönüş yarıçapı 10 m ise, arabanın merkezcil ivmesi nedir?
Çözüm: a = w^2*r = (2 rad/s)^2 * 10 m = 40 m/s^2
- Bir döner trafik lambası, sabit bir merkez etrafında dönerek hareket ediyor. Trafik lambasının açısal hızı 3 rad/s ve dönüş yarıçapı 5 m ise, trafik lambasının dönme periyodu nedir?
Çözüm: T = 2π/w = 2π/3 s
- Bir rulman, sabit bir merkez etrafında dönerek hareket ediyor. Rulmanın açısal hızı 4 rad/s ve dönüş yarıçapı 2 m ise, rulmanın lineer hızı nedir?
Çözüm: v = w*r = 4 rad/s * 2 m = 8 m/s
- Bir uçak, sabit bir merkez etrafında dönerek hareket ediyor. Uçağın açısal hızı 6 rad/s ve dönüş yarıçapı 100 m ise, uçağın merkezcil ivmesi nedir?
Çözüm: a = w^2*r = (6 rad/s)^2 * 100 m = 3600 m/s^2
- Bir bisiklet, sabit bir merkez etrafında dönerek hareket ediyor. Bisikletin açısal hızı 5 rad/s ve dönüş yarıçapı 4 m ise, bisikletin dönme periyodu nedir?
Çözüm: T = 2π/w = 2π/5 s
- Bir araba, sabit bir merkez etrafında dönerek hareket ediyor. Arabanın açısal hızı 2 rad/s ve dönüş yarıçapı 8 m ise, arabada etkin olan merkezkaç kuvveti nedir?
Çözüm: F = ma = mw^2r = m(2 rad/s)^2 * 8 m = 32m N
- Bir çemberin çapı 10 cm ve açısal hızı 4 rad/s ise, çemberin merkezindeki ivme nedir?
Çözüm: a = w^2*r = (4 rad/s)^2 * 0.05 m = 0.8 m/s^2
- Bir bisiklet, sabit bir merkez etrafında dönerek hareket ediyor. Bisikletin dönüş yarıçapı 2 m ve merkezcil ivmesi 5 m/s^2 ise, bisikletin açısal hızı nedir?
Çözüm: w = √(a/r) = √(5 m/s^2 / 2 m) = 1.58 rad/s
- Bir su damlası, sabit bir merkez etrafında dönerek hareket ediyor. Su damlasının dönüş yarıçapı 0.02 m ve açısal hızı 50 rad/s ise, su damlasının merkezkaç kuvveti nedir?
Çözüm: F = ma = mw^2r = m(50 rad/s)^2 * 0.02 m = 250mN
- Bir rulman, sabit bir merkez etrafında dönerek hareket ediyor. Rulmanın açısal hızı 10 rad/s ve dönüş yarıçapı 0.05 m ise, rulmanın lineer hızı nedir?
Çözüm: v = w*r = 10 rad/s * 0.05 m = 0.5 m/s
- Bir rulman, sabit bir merkez etrafında dönerek hareket ediyor. Rulmanın dönüş yarıçapı 0.03 m ve merkezcil ivmesi 15 m/s^2 ise, rulmanın dönme periyodu nedir?
Çözüm: T = 2π/√(a/r) = 2π/√(15 m/s^2 / 0.03 m) = 1.94 s
- Bir tekerlek, sabit bir merkez etrafında dönerek hareket ediyor. Tekerleğin dönüş yarıçapı 0.2 m ve dönme periyodu 5 s ise, tekerleğin açısal hızı nedir?
Çözüm: w = 2π/T = 2π/5 s = 1.26 rad/s
- Bir araba, sabit bir merkez etrafında dönerek hareket ediyor. Arabanın açısal hızı 3 rad/s ve dönüş yarıçapı 6 m ise, arabanın dönme periyodu nedir?
Çözüm: T = 2π/w = 2π/3 s = 2.09 s
- Bir kayış kasnağı, sabit bir merkez etrafında dönerek hareket ediyor. Kasnağın dönüş yarıçapı 0.1 m ve merkezcil ivmesi 10 m/s^2 ise, kasnağın açısal hızı nedir?
Çözüm: w = √(a/r) = √(10 m/s^2 / 0.1 m) = 10 rad/s
- Bir döner trafik lambası, sabit bir merkez etrafında dönerek hareket ediyor. Trafik lambasının açısal hızı 4 rad/s ve dönme periyodu 2 s ise, trafik lambasının dönüş yarıçapı nedir?
Çözüm: r = w*T/2π = 4 rad/s * 2 s / 2π = 1.27 m
Daha fazla soru örneği için yenisoruindir.com tavsiye edilir.